从一维回归任务说起

任务的定义和评价

给定一个输入空间和输出空间，我们想要通过输入空间中的变量预测输出空间中的变量，这就是ML和统计学中的回归任务。让我们考察一个简单的例子，输入空间、输出空间均连续一维的情况，即（单变量单值的）函数 f 的拟合。

我们假设数据按照如下的规律生成：y = f(x) + err, err ~ N(0, sigma)，即背后真实的分布 f 叠加与输入无关的高斯分布的噪音 err。我们希望设计一种算法 A，允许我们可以通过一定数量随机采样得到的已知数据（如前所述，这些数据包含噪音），构建一个尽量逼近 f(x) 的函数f_hat。

如何评价一个逼近函数 f_hat 的好坏？局部上（对于x0），我们用误差 f_hat(x0) – f(x0)；整体上，我们用函数空间中的度量 d(f, f_hat) 或者范数 ||f – f_hat||。

如何评价算法 A 的好坏？假想我们随机采集一系列的“训练集”，训练得到一系列的 f_hat 来评价。局部上，我们有一系列的预测值 f_hat_1(x0), f_hat_2(x0), … 以及一个真值 f(x0)，可以想到对这一系列的预测值服从某种分布，可以考察分布的期望和方差(variance)，其中期望减去真值可以得到偏差(bias)。整体上，或许可以用 ||f – f_hat|| 的期望值来衡量 A 好不好，这里不下定论。

方差和偏差关于模型能力的变化趋势

我们以多项式函数为例，假设 f 是2次多项式函数，以 f(x) = x*x – 2*x + 1, x in [0, 1] 为例。假设我们明智地选取了多项式拟合算法（等同于利用 1, x, x^2, …, x^p 这 p+1 个输入特征作线性回归）作为算法 A 。仍然有一个超参数待定，那就是拟合多项式（模型）的次数，以 degree=1,2,3,4,5 次为例，进行实验。选取 err ~ N(0, 0.1), 训练集大小为30。

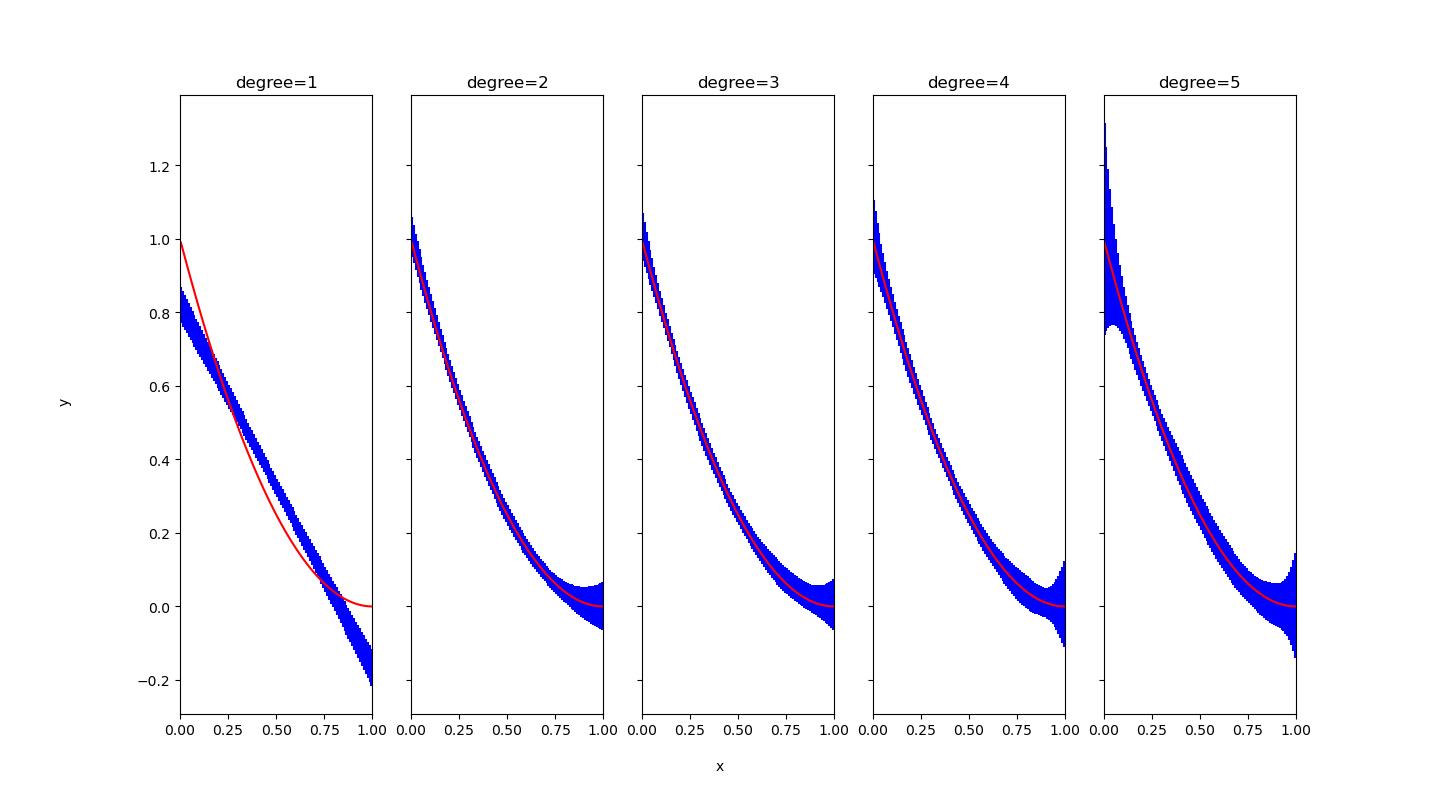
用红色线条表示 f(x)，蓝色线条及误差棒表示 f_hat(x) 的期望加减标准差，那么我们发现：N=1 时，由于预测函数必须是一条直线，预测值有偏差；N=2 以上，预测值的期望在哪里都是正确的，没有偏差。偏差随着模型的复杂或是接近数据真实的分布而向 0 靠拢（这是泛泛而论了，不意味着在每个 x0 处偏差都会向 0 靠拢）。另一方面，随着 N 的增长，误差棒较长的区域越来越多，可能的原因是随着模型的复杂，输出更容易受到“训练集”中噪音的干扰（这也是泛泛而论，不意味着在每个 x0 处方差都会扩大）。

这就是方差偏差取舍 bias-variance tradeoff 的经验之谈：模型越复杂，方差越大，偏差越小；反之亦然。

试分析泛化能力

由于未见的数据点也有噪声的存在，即使在最理想情况即 f_hat = f ，”测试误差“也不会为 0，而是达到一个非零的最小值，我们称此时的误差为 Bayes Error。f_hat 越接近 f，它就能越好地拟合未见的数据点，模型的泛化能力就越好。

我们可以计算 f_hat 在训练集上的误差，即训练误差。训练误差小，测试误差未必小，因为可能出现过拟合的情况，这是机器学习领域的经验常识。然而，如果试试看，我们在上面的例子中不太好构造训练误差小而测试误差大的反例 f(x)。例如，我们可以构造 f(x) = 1 or x is rational else 0，x 随机在有理数和无理数中取概率五五开。这样测试误差固然大，训练误差同样大。

之所以构造不出过拟合的反例，一是因为训练数据多而输入空间小，训练数据“铺满”了整个输入空间；二是因为模型太简单，模型参数的数量远小于训练数据点的个数。不知道是否正确的直觉，只要满足这两个条件，且禁止模型“储存输入样例并在推理时机械查表”的操作，那么我们就有理由期待模型能够泛化。

然而，在现实问题中输入空间是高维的，由于维数爆炸，第一条不被满足。在神经网络学习中，由于参数量巨大，第二条也未必被满足。

再谈神经网络的惊人表现

说到这里，该对前两篇“谈谈神经网络的惊人表现”的博文做一些回应和补充了。

与其说惊人的是模型没有死记硬背（这个不惊人，因为没有显式地设计这个操作），不如说惊人的是

1. 训练集上的优化能够进行下去（惊人的固然包括局部最优没有造成问题，更重要的是我们选择的 f_hat 刚好能够拟合问题中非常复杂的目标函数）
2. 在不符合”训练数据点铺满整个输入空间、模型参数量小于训练数据点“这两个条件的情况下模型依然泛化

Deep Learning Book 给出的一个论断，或许可以成为二者的共同原因：神经网络的层级结构允许它在维数爆炸的输入空间的各个区域之间建立关联，从而具有良好的拟合能力和泛化能力。

The answer to both of these questions—whether it is possible to represent a complicated function efficiently ^1, and whether it is possible for the estimated function to generalize well to new inputs ^2—is yes. The key insight is that a very large number of regions, such as O(2**k), can be defined with O(k) examples, so long as we introduce some dependencies between the regions through additional assumptions about the underlying data-generating distribution. In this way, we can actually generalize nonlocally.

Deep Learning Book, Chapter 5

在这里做一个不知道恰不恰当的比喻：剪纸创作中，对着层层对折的纸张下剪刀，再展开整张纸，会发现一刀剪出多个不临近的区域。在这里，整张纸对应输入空间，而”层层对折”对应了神经网络的层级结构。

附录：生成方差-偏差示意图的代码

"""
Illustrate the model bias and variance w.r.t. model capacity
"""

import random
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

random.seed(1)
N_test = 100

def generate_data():
    x = random.random()
    # ground truth
    y = x*x - 2 * x + 1
    # error follows gaussian distribution
    y = random.gauss(y, 0.1)
    return (x, y)

def gen_estimators(n_est, n_train, degree):
    test_xs = np.arange(N_test) * 0.01 + 0.005
    test_input = np.zeros((N_test, degree+1))
    for deg in range(degree+1):
        test_input[:,deg] = test_xs ** deg
    y_preds = np.zeros((n_est, N_test))
    for i_est in range(n_est):
        xs, ys = np.zeros((n_train,degree+1),float), np.zeros((n_train),float)
        for i in range(n_train):
            x, y = generate_data()
            for deg in range(degree+1):
                xs[i][deg] = x**deg
            ys[i] = y
        regr = linear_model.LinearRegression()
        regr.fit(xs, ys)
        y_preds[i_est] = regr.predict(test_input)
    return y_preds

def calc_mu_var(y_preds):
    var = np.var(y_preds, axis=0)
    mu = np.mean(y_preds, axis=0)
    return mu, var

def get_x_test_y_true():
    test_xs = (np.arange(N_test) + 0.5) / N_test
    return test_xs, np.square(test_xs) - 2 * test_xs + 1

def plot_models():
    N_est = 50 # Train N_est estimators
    N_train = 30 # For each estimator, use N_train training data points
    N_try_deg = 5
    xtest, ytrue = get_x_test_y_true()
    fig, axs = plt.subplots(ncols=N_try_deg, sharey=True, figsize=(6,6))
    for degree in range(1, N_try_deg+1):
        y_preds = gen_estimators(N_est, N_train, degree)
        mu, var = calc_mu_var(y_preds)
        axs[degree-1].errorbar(xtest, mu, yerr=np.sqrt(var), fmt='none', ecolor='blue')
        axs[degree-1].plot(xtest, ytrue, c='red')
        axs[degree-1].set_xlim(0,1)
        axs[degree-1].title.set_text(f"degree={degree}")
    fig.text(0.5, 0.04, 'x', ha='center')
    fig.text(0.04, 0.5, 'y', va='center', rotation='vertical')
    plt.show()

plot_models()