A picture is worth a thousand words

AI 作图领域，存在如下两种不同的思路：

以 Stable Diffusion 为首的扩散模型，使用一系列的 denoising step 将一张随机噪声图片逐步在 CLIP 引导下转换为成品图。
把图像切割为 token，以 token 为单位自回归式生成图像。”自回归” 这一块与语言模型原理相同。

用人类作图类比，Stable Diffusion 就好比这种涂鸦方法：先随机胡乱在画布上勾勒几笔，然后在它的基础上迭代改进画出大体的轮廓，最后精修画面中的细节——不断迭代。而以 token 为单位的图像生成就像画某种死板的工程示意图：从左到右，从上到下，逐片区域添加所需的元素。

Stable Diffusion 于 2022 年 8 月发布，一炮走红，和同年 11 月的 ChatGPT 发布二者一起令 2022 年成为 AI 突兀进入大众视野的元年。以 token 为单位的作图一直都不出圈，不过 2021 年的 DALL-E 用的就是它，发展到 2025 年 3 月 OAI 发布的 4o Image Generation 也有这种方法的影子，它的威力丝毫不弱。

沟通图片和 token 的桥梁

以 token 为单位自回归地生成图像，很重要的问题就是如何将 token 转换为图片。如果生成每个像素的 rgb，一个 256 x 256, 3 通道的图片也需要 262144 个 token，并不现实，更不用提难以训练等其它问题。

为了获得 token 到图片的映射，要转而挑战一个更广的问题，即图片和 token 之间的双向映射。这可以通过 VAE (Variational Autoencoder) 差分自编码器实现。DALL-E 的 VAE 就是这类方法中的一个典型。

VAE 组件的代码及 Jupyter Notebook 演示：https://github.com/openai/DALL-E
论文：Zero-Shot Text-to-Image Generation

一图即千言

DALL-E 将图片和 token 相互转换：把一张 256×256 像素的图片与一个元素取值自 {0,1,…,8191} 的 32×32 矩阵（或者说 1024 个 token 的序列）相互转换。

每个矩阵内元素模糊地对应图片中的一块区域 – 并非是每个元素掌管 8×8 区域这样的严格对应，而是说元素取值的影响是局部性的，如矩阵左上角元素大体上只影响图片左上角附近的区域。
因此，整张图片可以看成一个有序、有结构的 token 序列（矩阵），每个 token 的取值在 {0,1,…,8191} 之间

这种对应，恰好可以用 A picture (256×256 px) is worth a thousand (1024) words (|V|=8192)” 这句陈词滥调来形容。不是 “一图胜千言”，而是 “一图即千言”。

演示

使用仓库中的 Jupyter Notebook 来演示，

原始代码得到的 “Reconstructed image” 如图左上角所示，这个样例中输出的图片和原图几乎没有区别。在 z 变成 one-hot 之前把 z 打印出来，就可以直观看到 32×32 的 token 都有哪些。它的维数和值分别为：

torch.Size([1, 32, 32])
tensor([[[7522,  741,  119,  ...,  629, 4695, 4695],
         [ 782, 7459, 6832,  ..., 6913, 5215, 5887],
         [1580, 6382, 5768,  ..., 5677,  224, 2913],
         ...,
         [3990, 7130, 5047,  ..., 6027, 5770, 1212],
         [4898, 5659,  732,  ..., 5788, 6476, 6397],
         [2757, 3243, 5504,  ..., 5016, 1144, 7261]]])

如果将下标为 16, 16 的 token 设置为一个任意值，如 1026，则画面变为图右上角：画面中间有改变，符合每个 token 影响一个局部的预期。

尝试整个 sequence 上下、左右颠倒：z_mod = torch.from_numpy(z_index.numpy()[:, ::-1, ::-1].copy())。复原出来的图片并不是将原图上下左右颠倒，整个处理管线并不对称。

可以将两张图片的 token 矩阵表示剪切、拼接到一起，复原出的图片是某种缝合。

自编码器信息处理流

具体来说，怎么对应？考虑一个从左到右执行的 图片 - token - 原图片 的信息处理流程。先不谈 图片 - token 和 token - 图片 具体怎么实现，从整体看，这是一个典型的自编码器 (Autoencoder) 架构。简而言之，自编码器是被训练将输入复制到输出，而内部有一个隐藏层作为信息瓶颈的系统，在此就不详述了 – 对应到这里，输入和输出就是图片，隐藏层就是 32×32 的 token 矩阵。

我们从目标分布中采样图片，输入这个信息处理流程，令输出的图片尽可能接近输入图片，这样 图片 - token（编码）和 token - 图片（解码）这组编解码器就训练好了。这里我们假设了隐藏层是 32×32 矩阵，其中每个元素只能确定性地取一个值。在此基础上，我们让每个取值对应一张表（称为 codebook）中的一个向量，由于 token 一共有 8192 种可能取值，整个 codebook 就是 8192 个向量的集合。这个 codebook 就像语言模型中的 embedding layer，也是可调整参数的一部分；训练过程中也要加入 codebook 相关的 loss，不在此详述了。

具体映射：一个示例

处理图片，可以使用 CNN 来变更横纵尺寸以及 channel 数。例如，原始的图片就是 256 x 256 的，有 RGB 3 个 channel。再不妨设 Codebook 中有 V 个向量，每个向量维度为 D。考虑如下的例子：

实现 图片 - token 的编码：

输入：256 x 256 x 3 （RGB 三通道的图片）
CNN Encoder: 256 x 256 x 3 -> 32 x 32 x N（输出 channel 数量为 N）
量化：对 32 x 32 中的每个 N 维向量：
- 找到 codebook 中离它最近的向量，输出其下标。这要求 Codebook 中每个向量维度 D=N。V 不被 N 约束。这种方法被称为 VQ-VAE (Vector Quantized-Variational Autoencoder)，向量量化的变分自编码器。
- 或把这个 N 维向量看成 logits，也就是在 Codebook 向量上的一个分布（categorical distribution）。inference 时，对这 N 维进行 argmax，因此输出取值范围 V=N。D 并不被 N 约束。这种方法被称为 dVAE (Discrete Variational Autoencoder)。

用下标取向量 + CNN 来实现 token - 图片 的解码：

输入：32 x 32，输出 32 x 32 x D。对每个 token 查表将其替换为对应的 Codebook 向量即可。整个 Codebook 就是这步操作的 Embedding 矩阵。
- 实际中可以先将 32 x 32 的输入转换为 one-hot 格式：32 x 32 x N，然后用一个 1×1 convolution（实际上就是逐像素线性映射）将它转换到 32 x 32 x D。由于输入是 one-hot 的，这里线性映射 / 1×1 convolution 的权重矩阵 N x D 就是 Codebook 自身。
CNN Decoder: 32 x 32 x N -> 256 x 256 x 3

若不熟悉 CNN 对图片尺寸放缩以及 channel 数变化，可以参考这篇教程。

DALL-E 使用的架构

DALL-E 的编码器使用上文中提到的 d-VAE 风格的量化方法。在训练时，可以不用 argmax，而是对隐藏层做 Gumbel-softmax，仍然保留 32 x 32 x N 维的形状输入解码器来训练。

token 和图片之间的相互映射并非用朴素的 CNN，将卷积与尺寸放缩耦合；而是交替进行 1) 卷积等尺寸变换单元和 2) 下/上采样算子（downsampling / upsampling）的方法。具体而言

等尺寸变换的输出可以看成两部分的相加：a) skip connection，即直接拷贝输入的部分（如果 channel 数有变化，则要逐像素进行线性变换即 1×1 Convolution）b) 经过四层 CNN 卷积变换的部分，其中 CNN 网络的结构使得输入与输出维度相同
下采样使用 Max-pooling 最大池化；上采样使用 Nearest Up-sample，对于 DALL-E 而言由于放大倍数总是 2，因此相当于把先前一个 pixel 的向量在对应的 2×2 的新位置拷贝 4 份。

每交替一次，称为一个 group；而每个卷积等尺寸变换单元称为一个 block。因此一个 group 也就包括两个 block 和一个 up/down sample（有例外，有些 group 没有 up/down sample）。整体的示意图如下：

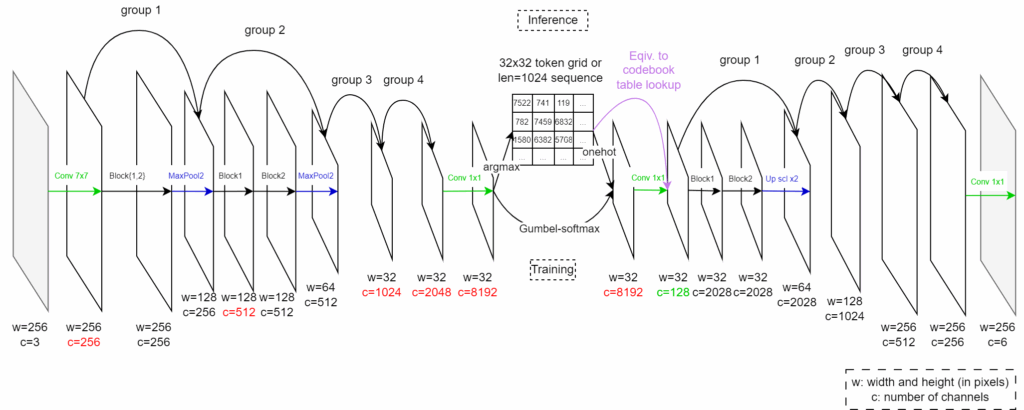
可以看出，这个 VAE 的 Codebook 有 V=8192 个向量，每个向量有 D=128 维；整个 Codebook 矩阵其实就是解码器第一个 Conv 1×1 的权重矩阵。

用自回归编码器建模图文联合分布

既然图片已经转换为 token 序列，那么把图片 token 的 Vocabulary 加入既有语言模型的 Vocabulary，用经典的自回归语言模型的方法（和模型：transformer）训练 {图片, 文字} 联合内容的生成就不难。

DALL-E 的联合训练方法

让模型自行决定何时生成图片、何时生成文字似乎比较困难（观察当下具有生图能力的 Chatbot，它们生成的文字和图片之间似乎都有外在设置的边界）；但我们可以先从 DALL-E 这个简单的场景开始：转述论文 2.2 节的内容，

BPE 编码文字得到的 16384 个 token 和图片的 8192 个 token 构成一个字母表
收集（图片 – 图片标题）对作为训练集。每一个训练样例，将图片标题 tokenize，作为输入的前 256 个 token（如溢出则阶段，不足则 pad）；将图片的长为 1024 的 token 序列表示串接在其后。
用这样的输入序列和交叉熵损失训练 transformer 即可

由于模型处理的序列的结构是固定的，推测可以在 logit 的层面上对图 token 或文 token 其中的任何一者进行屏蔽：对于前 256 个 token，屏蔽模型输出的图 token；对于后 1024 个 token，屏蔽模型输出的文 token，防止非法输出。

关于 gpt-4o 图片生成方法的猜测

OAI 在 2025 年 3 月发布 gpt-4o 的生图能力后，出现了很多对其技术实现的猜测。Introducing 4o Image Generation 这篇发布文自身就主动透露了很多信息，如第一个文生图例子抛出了大量思路。截取这个例子的 prompt：

(left)
"Transfer between Modalities:

Suppose we directly model
p(text, pixels, sound) [equation]
with one big autoregressive transformer.

Pros:
* image generation augmented with vast world knowledge
* next-level text rendering
* native in-context learning
* unified post-training stack

Cons:
* varying bit-rate across modalities
* compute not adaptive"

(Right)
"Fixes:
* model compressed representations
* compose autoregressive prior with a powerful decoder"

On the bottom right of the board, she draws a diagram:
"tokens -> [transformer] -> [diffusion] -> pixels"

这里提出的多模态实现方法和 DALL-E 是一脉相承的：

“model compressed representaions” 建模压缩后的表示：其实 VAE 的隐藏层就是某种压缩后的表示。这可以解决 “varying bit-rate across modalities” 跨模态比特率不一致这个问题。
“directly model p(text, pixels, sound) with one big autoregressive transformer”：抛开 sound，这也是 DALL-E 在做的事情。

diagram 言简意赅（尽管没有人保证这是 gpt-4o 生图实际上的实现方法）

tokens -> [transformer] -> [diffusion] -> pixels
用 transformers 读取 token，生成 token；对其中的 image token，用 diffusion 重绘为像素

原版 DALL-E 用的是仅 transformer + token 的组合。DALL-E 2 使用的是仅扩散模型的路线。现在，要同时利用 transformer + token 和扩散模型这两种思路。