本文从非分布式系统专业研究人员的视角,讲述分布式系统研究中一些基础问题和设计方法。写作大纲和具体协议或证明 完全启发自 / 参考了 Dahlia Malkhi 的 CMPSC 293B Foundations for Blockchains and Distributed Systems 课程。
用两个入门问题展示动机
两人相约问题
假设先前互不认识的 A、B 两个人需要合作,两人各自有一个只能按一次的按钮(即按下按钮是不可逆的),两人只有在未来的任意但相同的时间窗(如同一个小时)内按下各自的按钮,才算合作成功。两人只能通过收发邮政信件来通信。假设在这个世界中邮政服务是 “异步”(Asynchronous)的,即保证每封信件最终都会送到,但延迟可能任意高。
有没有一个协议,能够保证:
- 当 A 按下按钮,该时间窗内 B 必然也会按下按钮
- A、B 能够在有限时间内按下按钮合作成功
协议(拟)
开始草拟协议。假设 A 写信 L1 给 B,约定在某个时间窗 T 按下按钮。至此,A 能够下定决心在 T 按下按钮吗?不能,因为邮政服务可能将 L1 延迟到 T 结束之后送到 B,这种情况下 B 不会在 T 之内按下按钮,A 会扑空。
接上文,如果 T 之前 B 收到了 L1,回信 L2 给 A,表示确认收到。至此,B 能下定决心在 T 按下按钮吗?不能,因为邮政服务可能将 L2 延迟到 T 之后送给 A,依据上一段,这种情况下 A 还没有下定决心在 T 按下按钮,B 会扑空。
如此这般,即使在 T 之前 A 收到了 L2,A 也不能下定决心在 T 内按下按钮。以此类推,这样个协议是无法被构造出来的。
草拟这个协议的过程说明了异步通信下协议设计的困难之处。如果通信是同步的(延迟在 delta 时间内),问题可以朴素地解决。
通信可靠性的归类
我们看到通信的性质对问题至关重要,它分为下面几种:
- 同步(Synchronous)模型规定所有消息在延迟 delta 以内送达
- 异步(Asynchronous)模型规定所有消息可能经历任意长的延迟,但终究会送达
- 半同步(Partial Synchrony)模型规定 “全局稳定时刻 (Global Stabalization Time, GST)” 之前,消息的延迟没有上界;该时刻之后,所有消息在延迟 delta 内送达
拜占庭一致问题 (Byzantine Agreement)
“拜占庭将军问题” 一般而言指用自然语言描述的一类相似的情境:大意是,一组拜占庭的将军围困了一个要塞,驻扎在要塞的不同方位,将军两两之间可以通过不可靠的信使通信。这些将军需要决定要进攻还是撤退,但每个将军都有自己的想法;所有将军需要对进攻还是撤退达成共识,因为部分将军进攻、部分将军撤退会造成惨败。更糟糕的是有些将军可能会在通信中蓄意破坏共识。
一种简化和形式化拜占庭将军问题的命题是拜占庭一致问题。
假设有 n 个通过信道两两相连的实体,每个实体接受一个 0 或 1 的输入(对应将军本人的意见)。通过交流,每个实体需要不可逆地提交(commit)0 或 1(撤退或者进攻)。
你可以设计每个实体运行的协议,然而并非所有实体都正确地运行你设计的协议。正确运行协议的实体被称为诚实的(honest)实体;还有一部分的实体不依照你设计的协议运行,可能做任何事情,包括恶意破坏,这些实体称为拜占庭的(Byzantine)实体。
协议要达成的目标是:
- Agreement (一致性):所有 honest 实体提交的值相同。
- Validity (有效性):如果所有 honest 实体的输入都是 x,则所有 honest 实体都要提交 x。
- Termination (收敛性):存在某个时刻,所有 honest 实体都已经提交
这三条目标包含下面的含义:如果 honest 实体的输入并不统一,那么提交 0 或 1 都是可以的;然而所有 honest 实体都要在某一时刻前提交,且提交的值要相同。很多平凡的协议满足这个要求,比如 “所有 honest 实体都立刻提交0″,不过 Validity (有效性条件) 排除了这些平凡的协议。
对应回拜占庭将军问题,”一致性” 保证不会出现部分将军进攻、部分将军撤退的情况;”有效性” 保证了如果所有诚实将军对于进攻还是撤退的想法一致,那么这个意见会最终被执行。
事实上,不难证明无论通信有多可靠,只有当 Byzantine 实体的数量小于一半时,Byzantine Agreement 才可能实现。【附录1】
和三分之一的 Byzantine 实体在一起,怎能搞好 Byzantine Agreement 呢?
一个分布式系统中著名的不可能性结论是,在通信是半同步的情况下,如果 Byzantine 实体的数量达到所有实体数量的 1/3,则不存在解决 Byzantine Agreement (BA) 问题的协议。
可以参考这篇博文的讲解,或者原始文献 Consensus in the presence of partial synchrony 的 Theorem 4.4。由于这个文献是 1988 年发表的,而三个作者的姓氏是 Dwork, Lynch 和 Stockmeyer,所以这个结论也被称为 “DLS 1988″。
下面给出用反证法证明结论的大致思路。我们考虑简单版本的问题,作如下简化:
- 假设通信是异步的
- 假设只有 3 个实体(A, B, C)
假设其中有一个 Byzantine 实体,而存在满足要求的协议,我们设计出多个“世界”,在其中运行协议来反证。所有世界中,AB、BC的通信都是瞬间完成的,而AC通信被无限期延迟。
- 第一个世界中,A、B 获得输入1,C 是 Byzantine 的,表现为不响应。为了满足性质、A、B 需要在某一时刻之前 commit 1。
- 第二个世界中,B、C 获得输入0,A 是 Byzantine 的,表现为不响应。为了满足性质、B、C 需要在某一时刻之前commit 0。
- 第三个世界中,A 获得输入1、C 获得输入0。B 是 Byzantine 的,表现为欺骗:与 A 的通信模拟在第一个世界中的情况,与 C 的通信模拟处于第二个世界中”。
A 不能区分自己在第一个还是第三个世界中,C 不能区分自己在第二个还是第三个世界中。因此,在第三个世界中,A 会在某一个时刻前 commit 1,C 会在某一个时刻之前 commit 0,结果违反了一致性。

既然有了不可能性结论,那么对于 Byzantine 节点比例严格小于 1/3 的情况下,存在解决 Byzantine Agreement 的协议吗?一个被称为 “phase-king” 的协议可以解决这一问题(不过简化为同步通信的版本),具体协议就不在此说明了,可以参考这篇笔记。
发散性思考与现实启示
假设让现实中的三个人来扮演 A、B、C 来达到同样的目标,但允许三个人在同一个现场讨论,那么 honest 实体的策略是显然的:每个人都说一下自己收到的输入,然后统计,0 和 1 哪个值 “票数” 多就 commit 哪个值,用预先约定的默认值打破平票。使用群聊与现场讨论是同理的。
本质上,”同一个现场讨论” 或者 “群聊” 达成的效果就是 A 对 B 说了什么,在场/群里的 C 全都知道。达成共识在群里进行一切相关沟通,并忽略没有在群里公开说明的内容,这是对 honest 方最优的策略。这似乎对于团队高效合作有启示意义。
后文的 BFT 问题也可以概括为 “靠一群不可靠实体两两之间的不可靠通信,让其中honest 的实体对一个事件序列达成一致” 。不严谨地说,把事件序列视为群消息序列的话,BFT 的目标就是建立一个群聊。
拜占庭容错的共识问题 (BFT Consensus)
上述情境问题让我们有动机提出一个通用的问题框架:拜占庭容错共识 (Byzantine Fault Tolerance Consensus) 问题。
- 拜占庭容错,即一部分节点是 Byzantine 的
- 通信不可靠
- 共识(Consensus),指 honest 节点应该作为验证者(Validator)对一个序列达成一致。
验证者向序列中添加新区块,需要满足下面的条件:
- 一致性(Consistency / Safeness):所有 honest 节点看到的事件序列是一致的
- 活性(Liveness):网络应该能够处理请求,将合法的区块添加到序列中
依据通信可靠性的类别不同、可靠节点的比例不同,以及出错模式的不同,这个问题有难易不同的版本。关于出错模式,有
- 非 honest 节点行为不可预期
- 非 honest 节点宕机(crash),即在某个时刻后完全不响应的模式。这个模式更简单,因为节点出错后不会 “主动干扰其它网络中的其他节点” 。
比特币网络解决了 BFT 共识问题吗?
这个问题定义立刻让我们联想到比特币,它是一个去中心化的记账网络。比特币网络通过 “Proof of Work” 机制、最长链胜出机制和经济激励,在效果上解决了现实版本的 BFT 共识问题:
- 最长链胜出机制让每个 miner 有动机认定最长链为事件序列,并在它的基础上试图添加新区块。只要恶意攻击者掌握的算力小于 50%,就不会破坏一致性。
- 经济激励保证网络不断接受交易请求,将其添加到事件序列(账本)中。
只不过,比特币市场上事实上的算力集中(矿池的出现和流行)侵蚀了比特币的分布式特征。
分布式协议中的常见组件
在比特币出现之前,就有很多解决分布式问题的尝试。这些尝试不一定针对 BFT Concensus 问题,乃至解决的问题都相对独立、简化。然而,其协议设计中的设计模式有很强的通用性,为可以为后来的设计提供灵感,事实上是分布式协议设计的基础组件。
拜占庭广播,Dolev-Strong 和签名链
拜占庭广播(Byzantine Broadcast)问题
n 个节点中,第一个节点领导被指定为领导,接受输入 v = {0,1},然后试图将 v 广播给余下的节点。所有节点要不可逆地提交 0 或 1。我们希望达成:
- Agreement 一致性:不论领导是否 honest,所有 honest 节点提交的结果相同
- Validity 有效性:如果领导是 honest 的,所有 honest 节点都提交 v
- Termination 收敛性:存在某个时刻,所有 honest 实体都已经提交0或1
问题的关键在于,身在其中的节点不知道领导是否 honest,所以需要互相通信来验证领导是否可信,避免出现不一致的情况。
注:一般的拜占庭广播问题(BB)可以和拜占庭一致问题(BA)相互规约到对方,因为两者都是相当基础的问题。见【附录2】。
下面假设这 n 个节点之间可以两两同步通信,且所有节点预先接入了公钥基础设施(Public Key Infrastructure, PKI),允许节点利用自己的密钥对消息进行签名,以及验证其它节点的签名(对比公钥)。
Dolev-Strong 协议
设计思路是利用通信的同步性,设计若干回合。在多个回合之间,让 honest 方传播、延长如下的”签名链“。假设第 i 个节点对消息 m 的签名是 gi(m),注意到签名可以嵌套:
- 1-签名链由领导签名,是 g1(v),对输入值 v = {0,1} 的签名
- 2-签名链是对某个非领导节点对 1-签名链 g1(v) 的签名,比如对于 j!=1 的 gj(g1(v))
- 以此类推
- k-签名链必须在第 k+1 回合被接收,并且拥有 k 个互不相同的节点的签名
Dolve-Strong 协议可以容许任意 t<n 个 Byzantine 节点。容许 t 个 Byzantine 节点的协议如下:
Round 1: Commander signs and sends value to all parties
Round j=2 to t+2:
For a message m received in the previous round:
if m is a valid (j-1) sig chain on v not containing Pi's sig
Add v to the output set O, send gi(m) to other parties
Finally, if |O| = 1, output that value, else output a default value.通信是有限轮次的,协议的收敛性显然。下面证明协议的有效性。给定领导是 honest 的,它要依据协议给所有余下的节点发送且仅发送 g1(v)。
- 由于 Byzantine 节点没有领导的密钥,所以它无法构造始于 v’ != v 的签名链,所以每个 honest 节点的输出集 (output set) O 中不可能有 v’。
- 另一方面,容易看出每个 honest 节点第 2 轮就会将 v 加入输出集 O。
所以每个 honest 节点都会提交 v。
协议的一致性较难证明。关键在于做如下断言:如果任何一个 honest 节点在某回合将 v 加入输出集 O,则 v 一定已经或将要被所有的其它 honest 节点收到且加入输出集。这是因为:
- 在第 2,…t+1 回合,honest 节点在如此做后会向所有其余节点广播针对 v 的有效的签名链(其他节点将要收到)
- 在第 t+2 回合,如果 honest 收到有效的 t+1 签名链,则由于至多有 t 个 Byzantine 节点,至少有一个 honest 节点在更早的回合接收冰广播了它的签名链(其他节点已经收到)
因此,所有 honest 节点在协议结束时的输出集相同,提交的值也相同。
Dolev-Strong 协议最显著的设计就是签名链了。它的优点是容许任意多个 Byzantine 节点,缺点是指数的通信开销。

二元共识问题和 Commit-Adopt 设计
二元共识问题 (Binary Agreement)
问题的定义可以参考这篇博客,这个系列博文对这个问题做了很好的说明。有 n 个节点,每个节点是初始输入为 0 或 1 的自动机,自动机有一个特殊的、不可逆的动作即决定(decide)。在这里,我们仅考虑良性的出错模式,即宕机(crash),将允许宕机的节点的数目记为 f 。想要设计一个满足如下性质的协议:
- Termination 收敛性:所有不出错的节点都要 decide
- Agreement 一致性:所有不出错的节点都要 decide 同一个值
- Validity 有效性:如果所有不出错的节点初值都是 v,则它们都 decide(v)
不容许一人出错
这又是一个分布式系统中的著名不可能性结论:假设通信是异步的,任何容许(即使是一个)节点出现宕机故障的协议,必然存在一条无限执行、无法终结的执行路径。可以参考这篇博文的讲解,或者原始文献 Impossibility of Distributed Consensus with One Faulty Processs。由于这个文献是 1985 年发表的,而三个作者的姓氏是 Fischer, Lynch 和 Paterson,所以这个结论也被称为 “FLP 1985″。这里就不论述其证明了。
幸运的是,沿用异步通信的设定,假设所有节点有一个共享的硬币(所有节点投掷的结果相同),则我们可以设计出允许宕机的情况下以无限高的概率终结的协议。具体地,我们假设 f < n/2。
随机化共识协议(Randomized Consensus)
让我们草拟一个利用硬币的协议。所有节点广播它的初值;而所有节点都尝试接受 “其余存活节点” 的值,如果接收到的值一致为 v 则 decide(v);如果不一致,则投掷硬币,将硬币的结果作为决定。
这个设计的问题是我们不能确定有多少个存活节点。在等待到了 n-f 个消息后,要继续等待吗?
- 如果继续等待,则恰好有 f 个节点宕机的情况下会永远等下去。
- 如果不继续等待,马上 decide,则对于存活节点数量大于 n-f 的情况,一共可以接收到大于 n-f 个消息,接收到的值一致与否与接受消息的顺序有关,不同消息顺序会导致不同决定,违反一致性。例如,初始值多数为 0,少数为 1,有些节点收到 0 的全票,有些节点收到 01 混合的票,投掷硬币的结果不巧为 1。
我们需要一个节点在接收 n-f 个消息后立刻行动,但不立刻决定的设计。为此,考虑多个回合的设计,每个节点依据其回合之初的值行动,而在回合中可能改变它的取值。
Commit-Adopt 设计
在第一个阶段,每个节点广播自己回合之初的值,然后接收 n-f 个值,投出自己的票:n-f 个值一致则为该值投票,否则投票 “不在这回合决定”
round r, phase 1: # ratify phase
send (ROUND=r, MY=my_value) to all parties
wait for n-f MY messages # This will always complete
if all have the same value v, send (ROUND=r, VOTE=v)
else send (ROUND=r, VOTE=bottom) # bottom = "don't decide in this round"注意到 phase 1 中不可能同时出现 VOTE=0 和 VOTE=1:出现 VOTE=1 表示有 n-f 个节点的 MY=1,出现 VOTE=0 表示有 n-f 个节点的 MY=0,由于 2n-2f > n,如果两者都出现,就有节点的 MY 值既是 0 又是 1,矛盾。这保证了后面的协议算法是良定义的。
至此,思考几个问题,放在了【附录3】中。
第二个阶段依据受到的 VOTE 来 decide 或者采纳新的状态值。
round r, phase 2: # commit adopt phase
wait for n-f VOTE messages
if all have the same non-bottom value u, then decide(u) # commit
if any non-bottom value u is received, set my_value = u # adopt
else, set my_value = coin(ROUND=r)假设任何一个节点执行了 decide(u),那么投出的票中至少有 n-f 票 VOTE=u。由于 2n-2f>n,依据抽屉原理,任何一个节点受到的 n-f 票中必然有一票 VOTE=u。因此,在本回合所有节点要么 decide(u),要么将 MY 赋值为 u。后一种情况下,下一个回合所有节点都会 decide(u),协议结束。以上,我们已经论证了协议的一致性。
协议的有效性是显然的:所有不宕机的节点的 MY 值都是 v,协议会在第一回合结束时正确结束。
协议的收敛性最难讨论:
- 假设在开始时,初值为 0, 1 的各自刚好一半,那么 phase 1 中投出的 VOTE 全部为 bottom。这会导致 phase 2 中所有节点采用 coin 值,从而协议终结。
- 更难一些的情形,多数初值为 0,少数初值为 1,那么 phase 1 中投出的 VOTE 包括 0 和 bottom。不论票数分布怎样,phase 2 中有些节点收到的 n-f 个 VOTE 全部是 bottom,采用硬币值;剩下的节点采用 0。如果硬币值为 0,则下个回合结束;如果硬币值为1,则进入下一回合的相同讨论。(事实上,如果 VOTE=0 至少有 n-f 票,那么依据上面的论述,协议会在下一回合结束,不必依赖随机)
可以看出,在最坏的情形下,每回合也有 1/2 的概率保证在下个回合终结(所有节点 adopt 相同的值,因此协议的期望终结时间是有限的。
总结 Commit-Adopt 的设计思路
至此可以看出,所谓 “commit” 就是节点不可逆的 decide 动作,所谓 “adopt” 就是节点依据回合内受到的信息更新自己的取值。
上述协议之所以成立,关键在于:一个节点 Commit,则全体节点 Adopt。
法定人数(Quorum)
Quorum 是设计很多协议的基石。
从安全广播(Consistent BroadCast)问题引出法定人数
问题的定义和拜占庭广播类似,不过从通信条件更恶劣:从同步通信变成了异步通信。下面的协议可以在 f < n/3 个拜占庭节点的条件下,满足 Agreement 和 Validity(不一定满足 Termination)。为了简单起见,我们不把领导包含在 n 个节点之内。
协议设计如下:
- 领导应将初始值广播给其余所有节点
- 其余所有节点在接收到领导发来的第一个值 x 时,广播该值(ECHO, x);在接收到 n-f(多数)个相同取值的 (ECHO, y) 时,提交 y。
协议的确不满足 Termination:领导不发送任何消息,则没有节点能够提交。
协议的有效性容易验证:如果领导 honest,则 n-f 个 honest 节点会发送 (ECHO, m),f<n-f,Byzantine 的节点无法打断或阻止所有 honest 节点收到 n-f 个 ECHO m,从而提交 m。
证明协议的一致性:设任意两个 honest 节点分别提交了x、y,则由于 n > 3f+1,有至少 n-f 个节点 ECHO 了 x,有至少 n-f 个节点 ECHO 了 y,将这两组节点各自称为一个 Byzantine Quorom(法定人数)。它们的交集大小至少为 2n-2f-n = f+1,即交集中至少有一个 honest 节点。这个 honest 节点既 ECHO 了x,又 ECHO 了y,所以 x=y。
这就是“法定人数”的设计的妙处:两组“法定人数”的交集包含至少一个诚实节点。

Quorum 到底该含有多少个节点?
很多来源会将 Quorum 的大小定义为 2f+1,然而这是节点个数处于边缘即 n = 3f + 1 的特殊情况 – 在这个情况下,n-f = 2f+1,二者都可以说是 Quorum 的大小。
然而,当 n 远大于 3f+1 的情况下,一个 Quorum 该设计成多大呢,是 n-f,2f+1 还是别的?这要由 Quorum 的性质决定。假设 Quorum 包含 q 个节点:
- 两个 Quorum 的交集包含至少一个诚实节点:2q – n ≥ f + 1
- 一个隐含条件是,Quorum 不能太大,必须能够找到足够的诚实节点来组成一个 Quorom:q ≤ n – f
因此,在 (n+f+1)/2 向上取整 还有 n-f 之间的取值都是可行的选择。由于 n ≥ 3f + 1,这个区间是有意义的。
附录
附录1:BA 要求 Byzantine 节点少于一半
将 Byzantine 节点的数目记为 f,假设 f ≥ n/2。
- 诚实节点的数目为 n-f,将其集合记为 P1
- 我们有 f ≥ n-f 个 Byzantine 节点,其中匀出 n-f 个 Byzantine 节点专门用于欺骗,记为 P2;其余的 Byzantine 节点装死即可
对于任何协议,都可以构造如下两个世界来反证:
- 第一个世界中,P1 被输入 1,P2 正确运行协议但假装输入是 0
- 第二个世界中,P1 被输入 0,P2 正确运行协议但假装输入是 1
由于协议本身在 P1 和 P2 的并集上正确运行,所以它无法区分第一个世界和第二个世界,为了满足一致性,P1 和 P2 需要输出同一个值 v。若要在第一个世界中满足有效性,v 需要是 0,若要在第二个世界中满足有效性,v 需要是 1,因此协议不满足有效性。
附录2:BB 和 BA 的相互规约
参考这个讲义。
用 BB 解决 BA
把 BA 归约到 BB,即利用 BB 协议解决 BA 问题:
- 首先进行 n 个回合,第 j 个回合中第 j 个节点作为领导广播自己的值,BB 协议保证了所有节点认定第 j 个节点广播的值是同一个值。
- 随后,每个节点统计 n 轮广播中接收的 n 个值,进行多数投票。提交投票结果。
一致性很好保证,因为每个节点认定的 n 个值是相同的,投票结果自然相同。
在 BA 的 n>2f 大前提下,有效性很好论证:如果 n-f 个诚实节点全部接收到 v,它们都会正确地广播自己的值,从而有 n-f 票投给 v,是多数。
用 BA 解决 BB
把 BB 归约到 BA,即利用 BA 协议解决 BB 问题
- 领导应把自己的值广播给其余所有节点;其余所有节点应试图接收领导发送的第一个值,赋值给 v,若没有收到,则采用 v = 默认值。特别地,领导的 v 即自己的值。
- 所有节点(包括领导在内)运行 BA 协议,每个节点的输入是 v。
BA 协议的一致性保证了上述协议的一致性。有效性方面,如果领导是诚实节点,则显然每个节点的输入都是领导的值,BA 协议的有效性保证了上述协议的有效性。
解决 BB、BA 问题的通用框架(拟)
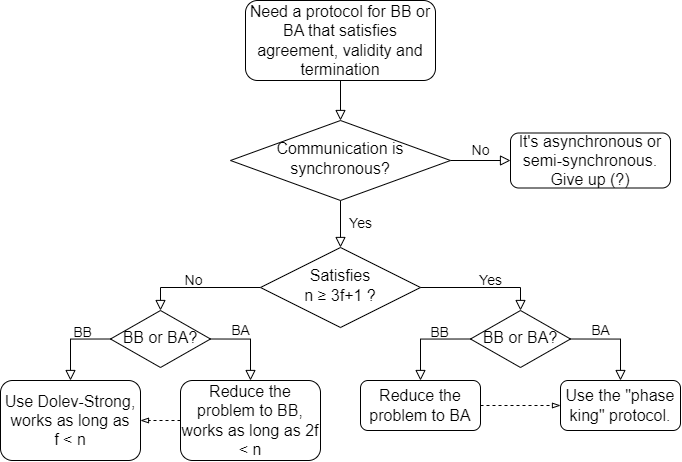
附录3:关于随机化共识协议的几个问题
Q:上面的论述中我们断言出现 VOTE=1,必然意味着有 n-f 个节点的 MY=1,这是为什么?
A:本问题中我们仅考虑宕机的出错模式,不考虑拜占庭错误,这意味着所有节点都执行全部或部分协议。依据协议,如果有节点执行到了 send (ROUND=r, VOTE=1),则该节点必然收到了 n-f 个不同来源的 MY=1;每个发送出 MY=1 的节点必然自己的值真的是 1。
Q:协议中的 wait for n-f MY messages 是阻塞的语句,可能出现永远阻塞在这里的情况吗?
A:不可能,因为至少有 n-f 个节点没有出错,这些节点发出的 MY 消息经过异步信道,终将抵达。反之,如果收到多于 n-f 个消息,则只有前 n-f 条消息才会被纳入考量,因为在那之后 wait 语句已经执行完成,前进到下一个语句。
Q:我们设定了通信是异步的,然而这里仍然使用了回合的设计,这成立吗?
A:由于通信是异步的,所以不存在一个全局的回合,每个节点需要维护自己的回合数 r,顺序执行各个回合的协议。正因如此,消息中才会标注出回合编号 ROUND。phase 2 中投掷共享硬币是以回合编号作为参数,在回合编号相同的情况下,所有节点投掷出的结果相同。由于回合编号相同并不意味着真实时间的相同,所以个人认为可以把共享硬币看作一个伪随机参数生成器,每前进一个回合就从生成器中取出一个随机数,由于所有节点预先设置为使用统一个伪随机数生成器,所以随机数序列 / 硬币投掷结果序列 是相同的。
Leave a Reply