随机化算法：从跳转表到分层小世界网络

本文可以视为“数据结构与算法”系列的延伸，在之前发布的相关博文基础上，介绍新的数据结构。“全序字典”问题和向量的近似 K 近邻问题可以被同一个简洁有力的思路解决。

跳转表

我们希望用数据结构实现下面的接口，我们将这种接口称为“全序字典”：

存储键值对，针对键查找值，用户保证键是全序的。查找、增加、删除的期望用时是 O(log n) 的。可以在 O(log n) 时间内找到最大的或最小的键，可以在 O(log n) 时间内找到某个键的“后继”或“前驱”。不支持循下标访问。

注意这个接口和“有序向量”的区别，后者的描述见下面，它可以用向量和二分查找算法朴素地实现。

用户保证元素必须全序。O(n) 插入元素，O(n) 删除元素，O(log n) 查找元素是否存在。O(1) 循下标访问第 k 个元素。

若要实现“全序字典”，最通常的想法是平衡二叉搜索树（例如 AVL 树）。然而除了它们之外，还有一种思路相当简洁的随机化算法 – 跳转表。

跳转表的二维结构

注：本小节即下面若干小节的内容整理自数据结构讲义，它可以从这个页面的“讲义历年存档”中获取。

跳转表有清晰的二维结构：从横向看，跳转表由多层构成，每层是一个链表；从纵向看，跳转表是一字排开、高矮不一的塔林，每座塔表示一个元素。使用维基百科的一张示意图：

横向的多层结构允许我们快速按键查找元素：我们从最顶层开始，逐层跳转。每一层中，不断循着链表向右查找，直到右边的元素大于我们要找的键；此时就下降一层。

关于塔的高度，它是在插入元素时从几何分布中随机采样得来的：以 p = 1/2 为例，则相当于从底层开始，不断抛硬币决定：1) 向上生长一层，或 2) 彻底停止生长。几何分布的期望是 1/p，因此在多层创建节点造成的存储开销也是这个值，是在可控范围内的。

跳转表的查询复杂度

根据上面对查询过程的描述，查询的复杂度取决于跳转表的层数和每层的跳转数。

假设一共有 n 个元素，则第 h 层有节点出现的概率的上界为 n * p^h。因此，我们可以以任意高的概率断言最高层不超过 O( log(n) )。这就限制住了跳转表的层数。

横向跳跃必然只能落到同等高度的塔上；否则，假若我们落脚在一个更高的塔上，我们在上一层的横向跳跃时早就该跳到这个落脚点了。向右数，在遇到更高的塔“撞墙”前，有多少座同等高度的塔？每数一个数，都有 P( h>k | h >=k ) = p 的概率”撞墙“。因此，每一层跳转的次数也符合几何分布，它的期望是 1/(1-p)。

因此，查询的复杂度有 log(n) / (1-p) 的上限。

跳转表的插入和删除

以新元素的键作为参数，调用查询算法，然后就可以在找到的位置上插入和删除元素了。对于插入或删除的元素，只需维护其每一层上的链表节点与左右的连接关系即可。

向量近邻搜索问题的网络解法

在文本、图像等信息检索中，我们常常将查询和候选文档表示为向量，选出距离查询最近的文档返回。问题是如何找到距离查询向量最近的 k 个候选向量？这被称为 K-NNS (k-Nearest Neighbor Search) 问题。如果允许近似和误差，则称为 K-ANNS (k-Approximate Nearest Neighbor Search) 问题。

我们希望依据用户给定的新向量查找其近邻的已有向量。通常而言，维护一个索引结构加速查找，这个结构可以动态增删已有的向量。

一种思路是，把“近邻”关系转换为每个维度上的”序“。然后，在目标向量附近建立一个”立方体“，套用”查找立方体中的点“的算法，比如：

范围树（range tree）。回忆范围树的思路是 ”树中套树“：第 i 个维度的上的范围树，其内部节点存储一个第 i+1 维度的范围树；直到最后一个维度，退化为二叉搜索树。它的构造时间/空间复杂度是 O(n (log n)^{d-1})，由于我们的向量表示通常是高维的，在构造范围树时就会遇到维数爆炸的问题，不可行。
kd 树：回忆 kd 树的思路是“每个维度轮流二分”。它的空间复杂度是 O(n) 的，即使在高维也可以建立起来。它的查询复杂度是 O(k + n^{1-1/d})。虽然最坏情况下的复杂度 O(n) 和暴力查询几乎没有区别，但实际上是否可能由于“立方体”很小而更快？

精确 K 近邻的 kd 树解法

对于 kd 树，直接套用“立方体查询”似乎不是解决近邻问题的最好方法。依据到目标向量的距离在 kd 树上进行 DFS 更适合我们的问题，简单直接。

参考这个讲义，具体的算法为：

从树根开始
不断下降，每次下降选择目标向量所在空间对应的子节点
到达叶子节点后，用叶子节点里的元素初始化候选元素堆，最远的候选元素在堆顶
不断回溯。对每个节点，试图将节点自身的“分界”元素加入候选元素堆。计算目标向量到分解平面的距离，如果该距离小于堆顶的距离，则再对另一侧没有访问过的子树做 DFS；否则，继续上探。

可以用下面的示意图辅助理解这个算法，图片来自 pyimagesearch.com。以 K=1 为例：

第 2, 3 步，我们到达A区域的叶子节点，将其中唯一一个向量作为当前最优
第 4 步，我们发现 Q 到 A-B 之间分界面的距离小于当前最优距离，因此再次对子树 B 做 DFS，实际上就是将当前最优更新为 (0.42, 0.65)
再次回溯，这次 Q 到 (AB)-(DC) 分界面的距离大于当前最优距离，搜索结束。

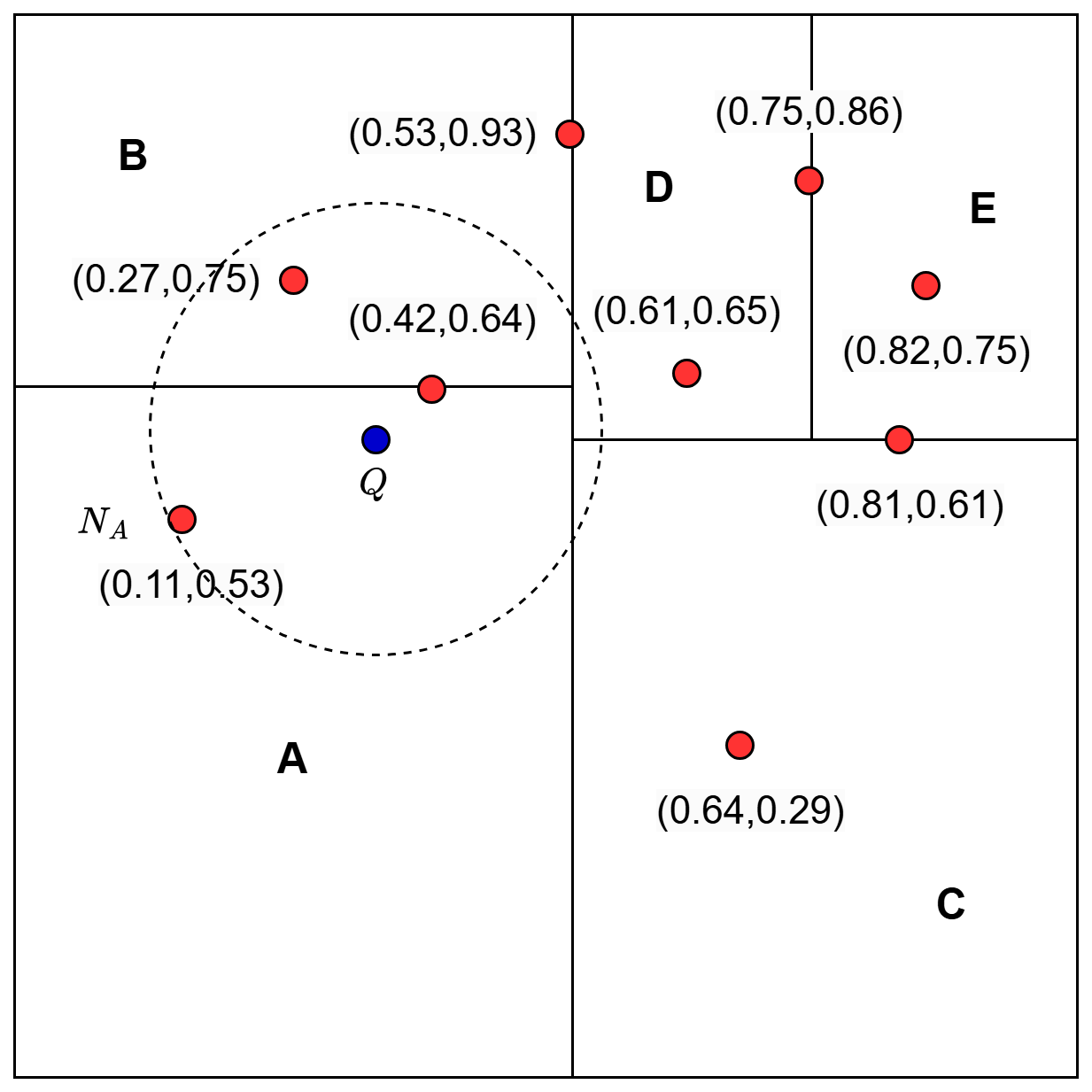
不难看出，这个算法可以求出精确的 K 近邻。只不过，它的查询复杂度无法被保证，只能希望它的实际运行速度较快。

近似 K 近邻的网络解法

如果我们不需要求出精确的 K 个最近邻居，允许一些误差，那么我们可以牺牲精确度，使用复杂度更低的算法。如果说“序”这种关系导出的是一字排开的结构，做一个自然的延伸，“近邻”关系导出的就是网络（或者说图论中的图）。

继续类比，在一字排开的结构上查找“大于”或者“小于”某个值的元素，可以从一个入口，不断走向前驱或者后继节点。那么，在网络上查找“临近”某个值的元素，可以从一个入口开始”导航”，不断走向当前节点的邻居，比如说，“贪心”地选择走向距离目标最近的邻居。这被称为贪心路由 “greedy routing”。

想要实现快速查找，基本上离不开某种显式或隐式的分层结构。研究人员最先利用的是隐式结构：小世界网络 (small world network) 短程和长程连接兼备，某种程度上就相当于分层结构——在导航时，贪心的选择会让你首先利用长程的连接迅速接近目的地，然后再用短程的连接精确缩进。这里的短程和长程，自然是依据向量空间中的范数确定的。

小世界网络的建立算法和我们“信息检索”的应用场景相匹配 – 它不需要先验信息且可以在线进行，每加入一个向量，我们只需把它和离它最近的 M 个邻居连接。不断加入向量的过程中，越早形成的连接，越容易充当长程连接的角色（因为当时的候选节点更少，所以选出的节点更远）。（参考论文）

分层可导航小世界网络

对于 K-ANNS 问题，如今被广泛采用的解法通过“分层”的方式，在上述小世界网络解法的基础上添加了显式结构。每一层都是一个小世界网络，越往上越网络的节点数越少，而每个向量都在前若干（不等）层的网络中作为节点出现，“生长”的高度服从几何分布… ——和跳转表的纵向结构完全吻合！这个方法被称为 Hierarchical Navigable Small World，缩写为 HNSW。使用原论文里的示意图：

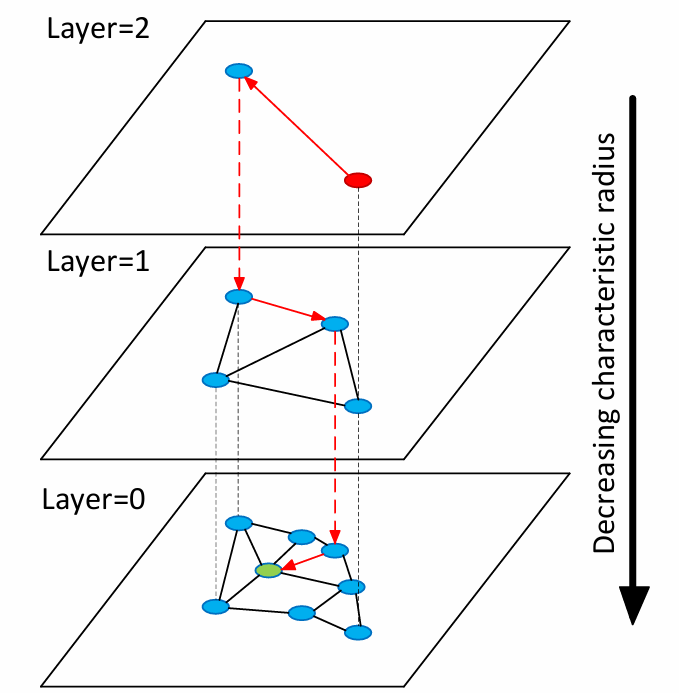
那么，查询算法、增删算法也可以一定程度上模仿跳转表了。

HNSW 的查询

从最高层的入口（entry point）开始，逐层下降，在每一层中使用贪心路由导航。用“导航”来描述 HNSW 的查询过程可能不准确，更准确的说法是“最佳优先搜索”（best first search），这在之前的图算法的博文中详述过。后者之所以不像导航，是因为它是无状态的：

Navigation / Routing 过程，“你”在任何时刻都出现在一个确定的位置，只能移动到相邻的位置
它也不像 DFS（包括递归式和模拟式）。例如它的模拟写法（常被称为 backtracking），可以棋类问题，在每一步都有一个棋盘状态，每一步只能改动一颗棋子
而最佳优先搜索，作为优先级搜索的一种，是靠优先级队列维护要访问的节点的。可能出现 “前一轮访问这里，后一轮访问很多跳之外的那里” 的情况。

具体的算法是 best-first search 的变种，在之前的博文中提到过，拷贝伪代码如下：

use entry point to initialize priority queue
let W be a candidate pool of max size K organized as a heap with worst on top
while priority queue is not empty
  pop node v with top priority
  mark v as visited
  if v is worse than every candidate in W:
    break
  for each neighbor u of v who is not visited:
    mark u as visited
    if u is better than the worst candidate in W
      push u to W
      push u to priority queue

每一层 best-first search，可以接受多个入口 (entry point)，也可以输出多个（这里是 K 个）候选向量。因此，我们可以把上一层输出的候选向量当成下一层的入口。实际的算法中，逐层下降的过程均使用 K=1，只有最底层输出 K>1（等于 k-NN 问题定义中的 k）个候选向量。

注意：因为前面所描述的原因，K=1 的情形并不能实现为 “每步只看眼前邻居，一旦邻居都比自己更远就停止”。

HNSW 的插入

首先根据几何分布生成新向量的“高度”。

然后是“检索”的步骤，从最高层“下降”到这个高度，每一层使用 best-first search 输出 K=1 个候选向量，得到一个新向量高度的 entry point。

自新向量的高度及以下的每一层，我们都需要实际插入这个新向量，因此需要选择它的 M 个邻居。方法即选定一个 K>M 来逐层下降，然后在每一层输出的候选向量中挑出 K 个最近的邻居（或者使用其它经验准则）和当前向量连接。

上述查询、插入算法的细节和伪代码可以参考论文。最后，附上一个 Python 代码仓库，包含对分层可导航小世界网络（HNSW）的 proof of concept 实现；HNSW 的高性能实现可以参考 FAISS 库，它是基于 C++ 的。